赌徒输光原理坐标图揭示的可怕真相

或许有人会疑惑：难道就没有一个公平的赌博游戏吗？设想一个场景：有一个良心老板，他不从中抽水，只是为赌徒们提供一个公平的游戏平台。然而，即便是在这样的公平游戏中，赌徒如果持续参与赌博，最终也难免遭遇倾家荡产的命运。这就是赌徒输光原理。

举个例子来说明：假设有一个公正的赌博游戏，在每一局中，赌客有50%的机会赢得1元，也有50%的机会输掉1元。赌客初始时有A元，他会在两种情况下停止赌博：一是输光所有的钱，二是赢得B元。那么，他最终输光所有钱而停止赌博的概率是多少呢？

我们可以用一个数学模型来描述这个问题。想象一个数轴，上面有0、1、2、3…B，一共B+1个位置。赌客开始时位于A位置。他每次都会随机向左或向右移动一格，直到到达0位置或B位置。那么，赌客最终到达0位置而停止赌博的概率是多少呢？

要解答这个问题并不复杂。我们可以设赌客有n元时，输光离场的概率是P(n)。根据游戏规则，如果n=0，赌客就会输光离场，所以P(0)=100%；而如果赌客有了B元，他就会满意地离场，因此P(B)=0。

在每一局游戏中，赌客都有50%的概率赢或输1元钱，也就是说，赌客的钱n有50%的可能变为n+1，也有50%的可能变为n-1。因此，我们可以得出一个公式：P(n)=50%×P(n+1)+50%×P(n-1)。

将这个公式进行变形，我们可以得到一个等差数列的关系式。通过这个关系式，我们可以发现P(n)这个数列是一个逐渐减小的等差数列，每一项都比它的前一项少1/B。

最后，我们可以根据这个等差数列的关系式，画出一个输光概率P(n)与现在资金量n的关系图。通过这个图，我们可以很容易地计算出当赌客的资金n=A时，他输光的概率P(A)=1-A/B。也就是说，输光的概率等于1减去你现在拥有的钱A除以你希望赢得的钱B。

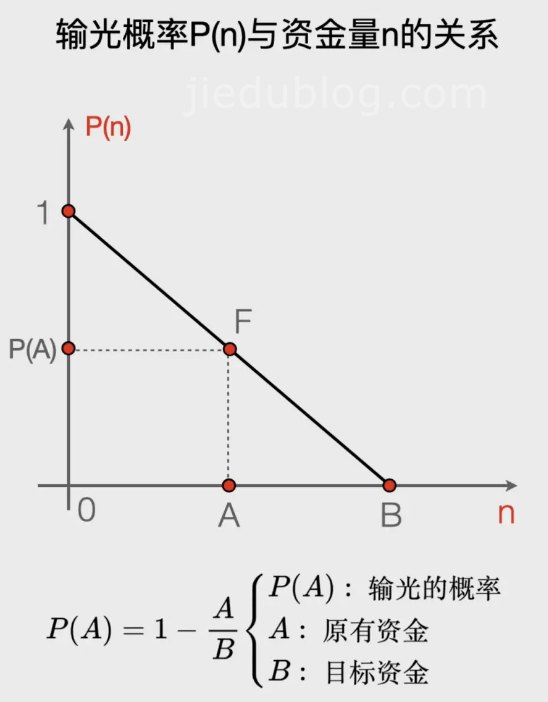
对这个结果进行一些讨论：如果你手头有100元，而你的目标是赢得120元就退出，那么A=100，B=120，此时你输光的概率是1/6；如果你的目标是赢得200元再退出，那么A=100，B=200，此时你输光的概率是1/2；而如果你的目标是赢得1000元再退出，那么A=100，B=1000，此时你输光的概率高达9/10。

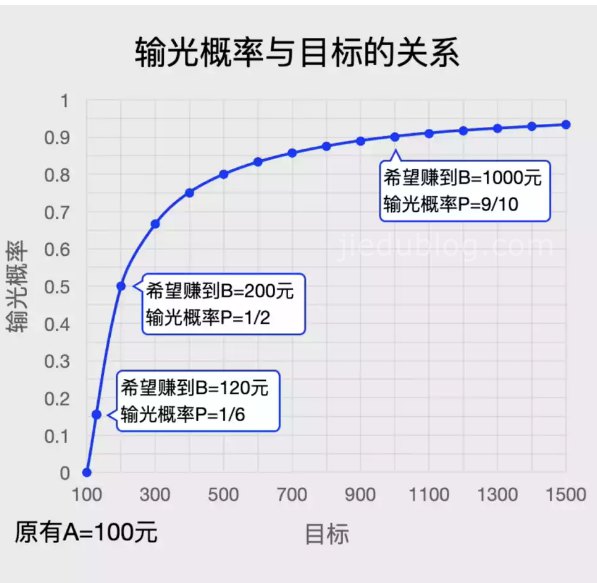
你会发现：你的目标越大，输光的概率也就越大。而如果你一直赌下去，无论赢了多少钱都不退出的话，那么最终你输光的概率将会是100%。这就是赌徒输光原理的残酷现实：久赌无赢家！

在赌徒与赌场老板的对赌中，即使是一个公平的游戏，由于赌场的资金量远远大于赌徒，赌徒几乎不可能将赌场赢到破产。最终，赌徒一定会输光所有的钱而离场。

作者：彻底戒赌不复赌

戒赌论坛博客 戒赌社区老哥故事 帮助沉浮赌海的人上岸 站点 QQ交谈